sinx/xのx→0の極限を計算してみましょう。
sinx/xのx→0の極限は単純に極限の計算に頻出であるだけでなく、sinxをはじめとした三角関数の微分に必要な極限です。
証明が阪大・名古屋市立大などでの出題実績もあるので手順から覚えておくべきです。
方針
以下のように図形をかき、図形の面積を考えることにより不等式をつくり、はさみうちの原理を利用します。

sinx/xのx→0の極限の計算
上記のように半径1の円で中心を点Oとし、円上に点A、点Bをとります。また、点Bにおける円の接線と線分OAの延長との交点をPとします。
∠AOB=xとおきます。
このとき、三角形OAB、三角形OPB、おうぎ形OABの面積を計算します。
三角形OABの面積
OA、OBはそれぞれ円の半径であって、なす角がxであるので、
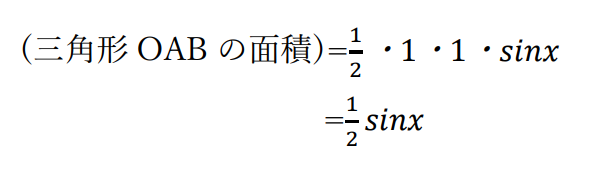
三角形OPBの面積
BPが円の接線なので、∠PBA=90°です。
またOBは円の半径1です。
線分PBの長さは、OPBが直角三角形なので
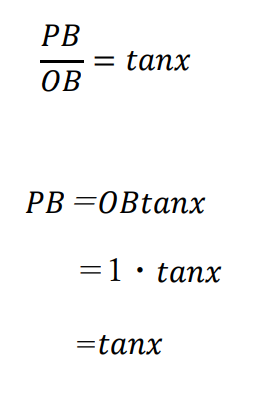
よって、三角形OPBの面積は、
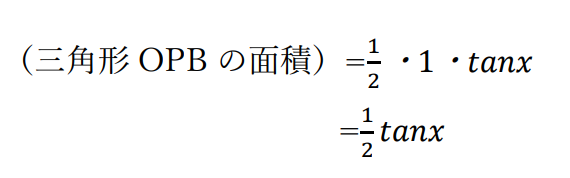
扇形OABの面積
扇形OABの面積は、OA、OBそれぞれが半径でなす角がxなので、
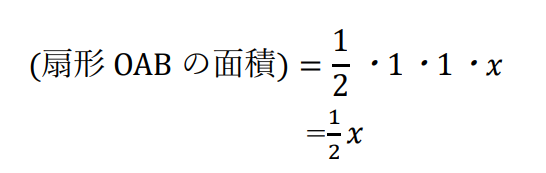
不等式をつくる
図から、(三角形OABの面積)<(扇形OABの面積)<(三角形POBの面積)なので、不等式
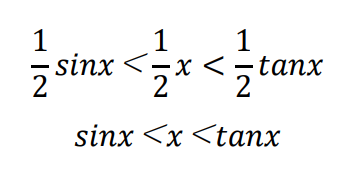
が成立します。
逆数をとってsinx(>0)をかけると、
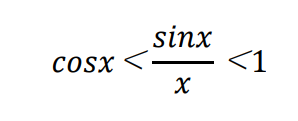
ここで、cosxのx→0の極限は簡単にわかります。
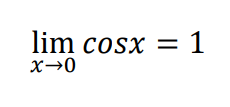
なので、はさみうちの原理により
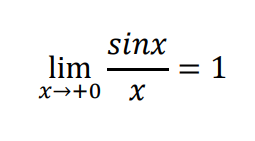
と計算できました。
sinx/xのx→-0の極限
+側からの極限はわかったので-側からの極限も考えます。
これは+側からの極限がわかれば式変形するだけで、
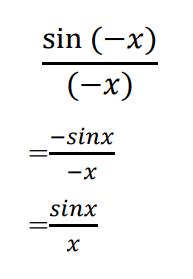
より
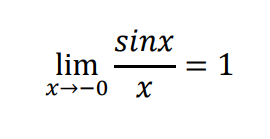
+側からの極限と-側からの極限が一致することがたしかめられたので、
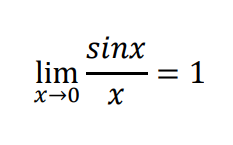
と計算できました。


コメント