三角関数の微分法

三角関数の微分について考えましょう。

ここではsinx/xのx→0の極限値が1であることは証明なしに用います。

証明は以下の記事にあります。

sinx/xの極限の計算

sinx/xのx→0の極限を計算してみましょう。sinx/xのx→0の極限は単純に極限の計算に頻出であるだけでなく、sinxをはじめとした三角関数の微分に必要な極限です。証明が阪大・名古屋市立大などでの出題実績もあ...

moshipro.net

2021.04.20

sinxの微分

微分の定義式

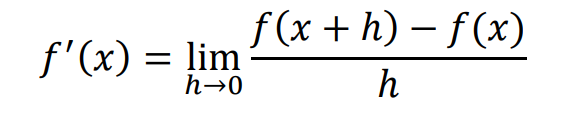
にあてはめて計算します。

sinxで微分の定義にあてはめると、

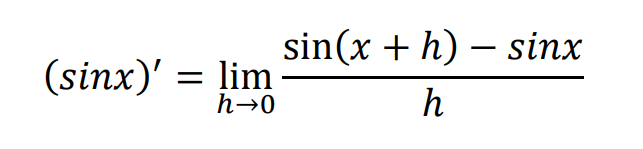
三角関数の加法定理を用いて展開し、sinxとcosxでまとめます。

ここで、

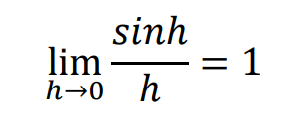
なので、

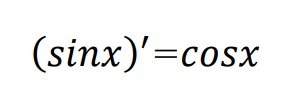
となります。

cosxの微分

cosxの微分も、sinxの微分と同様に定義から計算します。

加法定理を使いまとめるところまでsinxの微分と同じです。

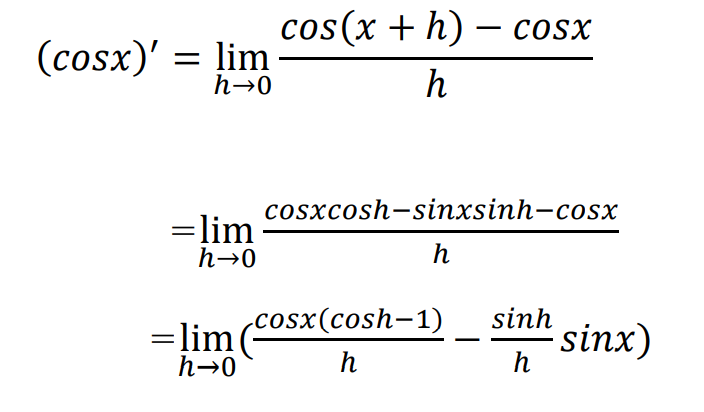
ここで、

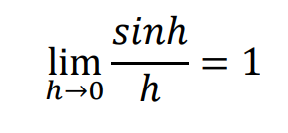
なので、

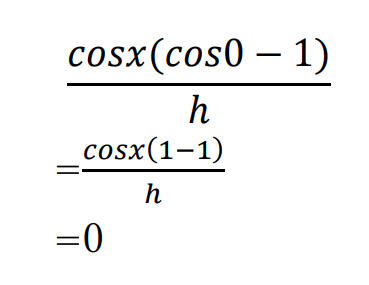
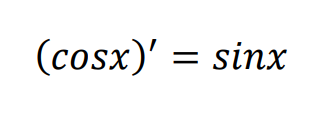
とわかります。

tanxの微分

tanxの微分は、定義にあてはめて計算するとややこしくなるので、三角関数の相互関係を使い

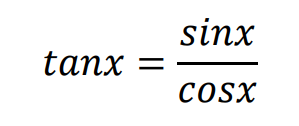
と変形します。

こうするとここまで計算したsinx,cosxの微分と商の微分法の公式

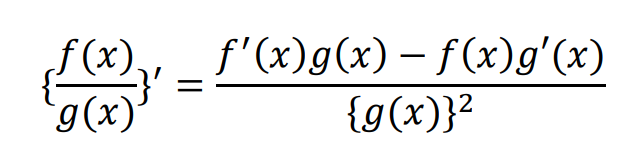
で微分しやすくなります。

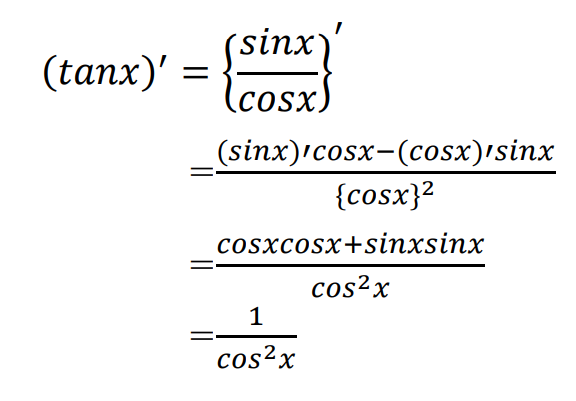
練習問題

練習問題の略解

(1) y’=2sin(2x+3)

(2) y’=-3cos(3x-1)

(3) y’=2/cos^2(2x-7)