数学Ⅰの三角比の円に内接する四角形の問題について解説します。
三角比の円に内接する四角形の問題は定期テスト応用~入試標準レベルで頻出です。
具体的問題はこちら。

正解にたどり着くのにいくつかポイントがありますので実際に解いてみましょう。
まずは与えられた条件から図を書きます。対角線を求めよといわれているので対角線も引いておきます。
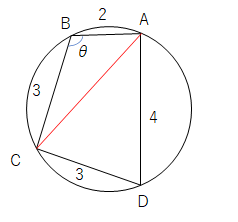
まずは対角線ACを求めたいですよね。
対角線を引いたことでちょうど三角形ができたので
∠ABC=θとおいて三角形ABCに対して余弦定理を適用すると、
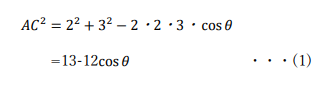
さて、この式だけではACとcosθの2つがわからないので、解けません。
もう一つ式が欲しいところ。
そこで2つのポイントからもう一つ式を出してきましょう。
- 円に内接する四角形は対角の和が180°になる
- cos(180°-θ)=-cosθ

円に内接する四角形は対角の和が180°になることから、∠ABCの対角である∠CDAは(180-θ)°であることになります。
ここで三角形ACDに余弦定理を適用してみると、
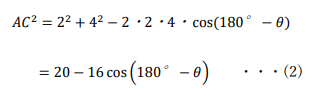
ここで2.のポイント
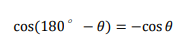
の関係があることから(2)の式は

と変形することができます。
これで未知数2つに式2つとなり方程式が解けますね。
解いてみると、
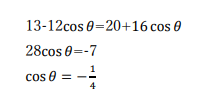
これを式(1)に代入して、
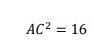

とりあえず未知の角度をθとおいてみることと、円の性質、三角比の性質からもう一つ関係式を持ってくることがポイントでした。


コメント