座標平面状の3点を結んでできる三角形の面積を計算してみましょう。
点の1つが原点である場合
平行移動させても面積は変わらないので、点の1つを原点に移動させ、
移動させたあとの各点をO(0,0),A(a,b),B(c,d)とおきます。

三角形の面積の公式『底辺×高さ÷2』
を使えれば三角形の面積が計算できるので、三角形OABにおいて底辺と高さを考えましょう。
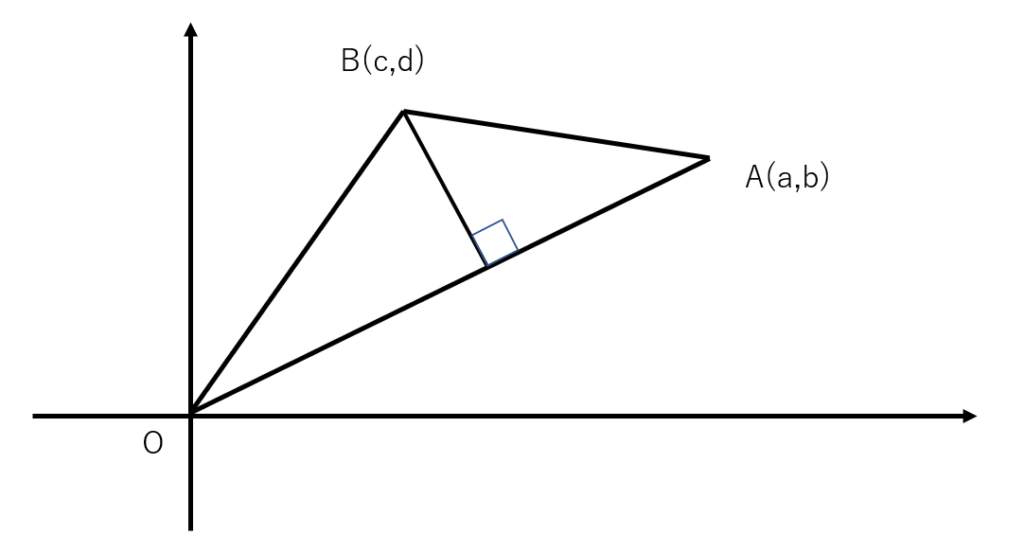
底辺
辺OAを三角形の底辺とみなすと、辺OAの長さは座標平面状での点Oと点Aの距離といえるので、
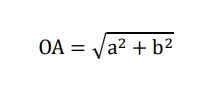
となります。
高さ
高さとは線分OAと点Bとの点と直線の距離ですから、点と直線の距離の公式にあてはめられますね。
線分OAをあらわす方程式は、点O(0,0)と点A(a,b)を通ることから、

よって三角形の高さh(=点Bと線分OAの距離)は
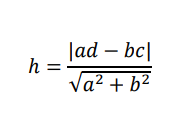
三角形の面積
三角形の底辺と高さが座標を使って表せたので、三角形の面積をSとするとSが座標だけで表現できて、
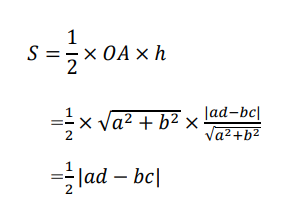
よって、
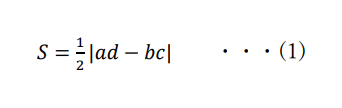
となります。
例題
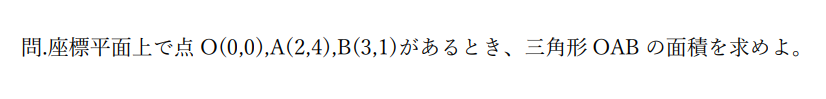
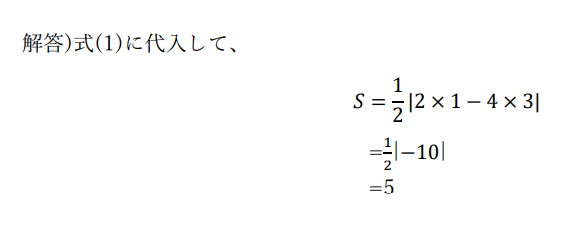
補足
同様にして3点のすべてが原点にない場合の面積公式もつくることができますが、
いずれか1点が原点になるように平行移動してしまえば簡単な式(1)を適用できるのでそこまでする手間は必要ないでしょう。


コメント