理想気体は理想気体の状態方程式PV=nRTに従っていました。
しかし理想気体は
・分子間力がはたらかない
・分子に体積がない
という2つの仮定のもと成り立っているので、実在の気体では理想気体の状態方程式からずれが生じてきました。
そのためより正確に実在気体の挙動を記述するために様々な式が提案されてきました。
完全に実在気体の挙動を表現できる式は発見されておらず、目的によってより都合のよい式を使用しています。
種々存在する状態方程式の中でも特に有名なファンデルワールスの状態方程式を解説します。
ファンデルワールスの状態方程式
ファンデルワールスの式は理想気体の状態方程式において、分子間力と分子の体積を考慮して導出された式です。
比較的簡単でかつ理想気体の状態方程式よりも正確に記述できることから現在でも頻繁に扱われています。
ファンデルワールスの式の導出
ファンデルワールスの式は理想気体の状態方程式に「体積」の項と「分子間力」の項を考慮するようにすることで導き出されます。
体積の影響の補正
ある気体を体積Vの容器に入れると、分子の体積を無視するなら、
気体分子が自由に動ける体積がVであると考えられます。
しかし、分子の体積を無視できないとすると気体分子が自由に動ける体積はVから分子の体積を取り除いたものだと考えることができます。これを排除体積といいます。
排除体積は分子の体積と関係しますが、完全に分子の体積とは一致しません。(分子間の相互作用も関係してくるからです。)
一分子あたりの排除体積をbとすると、n[mol]の排除体積はnbとなり、
分子が自由に動ける体積はV-nbとなります。
理想気体の状態方程式において分子の体積を考慮するると、

となります。
bの値は気体の種類にかかわらない定数で実験的に決定します。
分子間力の影響の補正
分子間力は気体を閉じ込めるのに必要な圧力を減少させるので、Pに対して補正項を導入します。
分子間力はある分子の周辺に存在する別の分子とはたらくと考えます。
体積Vの中に気体分子がn[mol]あると考えると単位体積あたりの分子数はn/Vに比例し、ある分子の周辺に存在する分子数もn/Vに比例します。
すべての分子による分子間力は実験的に求められる比例定数aを用いて
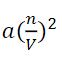
とかけるので、圧力項を補正すると
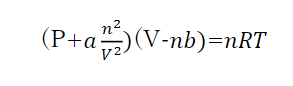
と表すことができます。
これをファンデルワールスの方程式といいます。
練習問題

練習問題の答え

ファンデルワールスの状態方程式の入試問題
ファンデルワールスの状態方程式は大学入試でも少なからず出題されます。
厳密な扱いは大学レベルになるので、比較的単純な計算問題が主になります。
練習問題として入試問題を紹介します。
2022 千葉大 第1問
大学入試でもすくなからず出題されますが
厳密な理論の扱いは大学レベルの内容となるので現実的には単純な計算問題が考えられます。


コメント