JR東海道新幹線・山陽新幹線・九州新幹線では2020年5月20日乗車分から、荷物の3辺の合計の長さが160cmを超える荷物を持ち込むときには事前予約が必要になりました。

こうなってくるとちょっと思ってくるのは
「予約不要な範囲内でできるだけ大きい荷物をもちこみたい!」
ということですよね!
3辺合計が160cmの条件でどれだけ大きい荷物を持ち込めるのか
高校数学を利用して計算してみましょう。
数学的に言い換える
体積が最大になるときの3辺の長さを求めたいわけなので、それぞれを未知数(JR東海のホームページに合わせてA,B,C)をおきます。
求めたい体積は底面積×高さで求められるので、結局はこういうことですね。

体積が最大になるときの3辺の長さを求めよう。
文字が3つありますが条件が一つついているので、文字を一つ消去できますね。

文字が一つ消えたので、ここからさらに文字を一つ固定します。
ここではBを固定すればyがAの二次関数になりますね。
平方完成することができて、
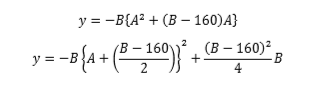
平方完成結果から
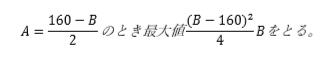
とわかりますね!
ここからはこの条件のもとで、Bだけで表されたyの最大値を求めましょう。
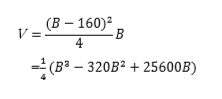
最大値VがBの三次関数になっているので、微分してグラフをかければ最大値と最大値をとるBの値がわかりそうですね!
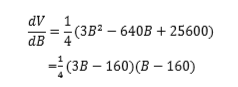
0≦B≦160の範囲で増減表とグラフを書いてみると、
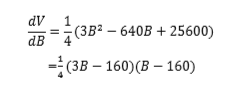

なので、
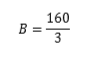
で極大値かつ最大値を取りますね。
このとき、A,Cは
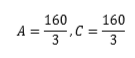
であって、最大値は
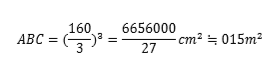
となります。
3辺をどうすればいいか?
というわけで持ち込める荷物の量をできるだけ増やすためには、3辺を同じにする(立方体にする)ことがよいことがわかりました。
実は合計が160cmのときに限らず3辺の合計を固定して体積を最大にするなら、立方体にするのがいいことが同じ計算でわかります。


コメント