この記事では有機化合物の構造決定問題に便利な不飽和度という考え方を解説します。
不飽和度を授業で習った人はそこまで多くはないかもしれません。
教科書には載ってないし、不飽和度自体はつかわなくても問題は解けますからね。
しかし有機化合物の構造決定問題を解くのにめちゃくちゃ力を発揮するので、ぜひ覚えて役立ててください。
不飽和度とは?
不飽和度とは、有機化合物に二重結合、三重結合や環状構造がどれだけあるかを示したものです。
つまり、不飽和度を求めることができればその有機化合物内にどれだけ二重結合・三重結合・環状構造があるかがわかります。
ということは有機化合物の構造決定問題を解くときに不飽和度を求めることで、実際にいろいろ書いてみなくてもある程度構造を予測しやすくなる。
という点でとっても便利です。
不飽和度の考え方
飽和化合物が不飽和になると水素原子の数が減ります。
このとき、二重結合あるいは環状構造が1つできるごとに水素原子が2個ずつ減っていきますね。(三重結合は二重結合2つ分と考えます。)
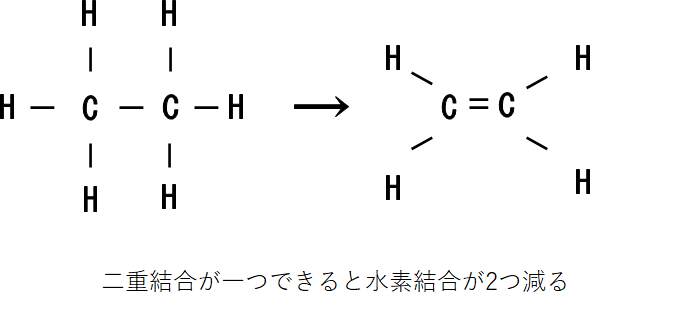
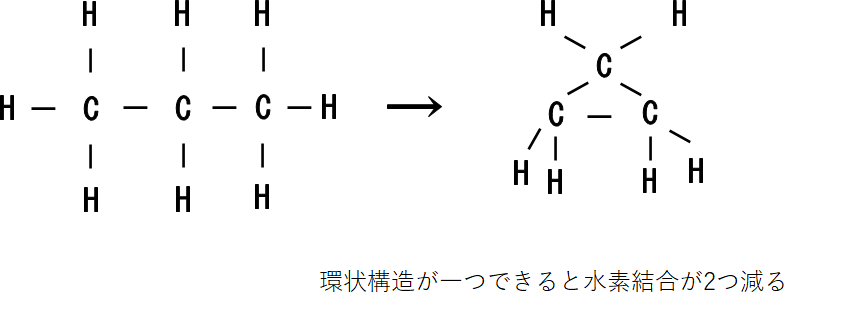
ということは、飽和している状態を考えたとき分子が持ちうる水素原子の数から実際に分子が持っている水素原子を引いて、2で割ったらそれが分子の二重結合、環状結合の数ということになります。
これを不飽和度と呼びます。

というわけで飽和状態での水素原子の数を数えることができれば、実際に分子がもつ水素原子の数はわかるので不飽和度=分子中の二重結合と環状構造の数がわかりますね!
飽和状態での水素原子の数え方
では飽和状態での水素原子の数え方を見てみましょう。
炭素について
炭素の数がnのとき、飽和状態では水素は2n+2個になります。(アルカンを想像するといいですね)
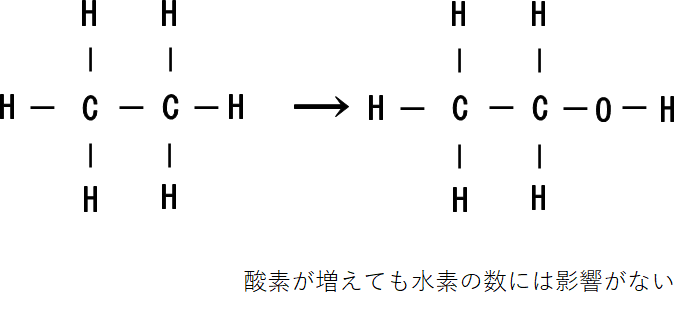
酸素について
酸素については、いくつ増えても飽和状態の時の水素の数に影響は与えません。
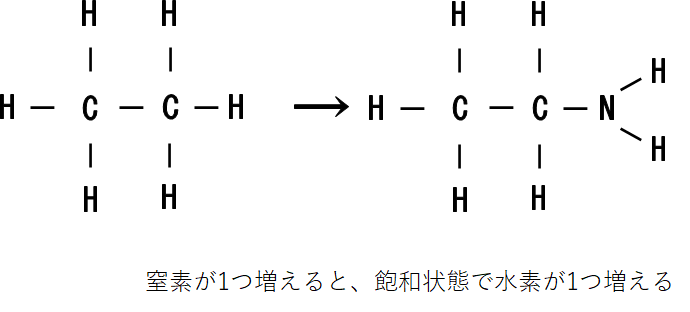
窒素について
窒素については、結合の手が3本あるので窒素原子が1つ増えると、飽和状態では水素原子が1つ増えます。
まとめると
飽和状態の水素の数は
(炭素の数)×2+2+(窒素の数)
になるので、最終的に不飽和度を調べる式は以下のように決められますね!

例題
というわけで2つほど例題を用意したので、見てみましょう。

(1)
不飽和度の式に代入すればいいですね。
(2×4+2-8)÷2=1
不飽和度は1です。
二重結合が1つまたは環状構造を1つもちますね。
(2)これも不飽和度の式に代入です。
(2×6+2+1-5)÷2=5
で不飽和度が5ですね。
大学入試問題では、不飽和度が4以上ならほぼベンゼン関連化合物になります。(ベンゼンは環状構造1つ、2重結合3つで不飽和度4に相当しますね。)
【関連記事】


コメント