気体の状態方程式
ボイルの法則:温度一定では気体の体積は圧力に反比例する
シャルルの法則:圧力一定では気体の体積は絶対温度に比例する
アボガドロの法則:温度・圧力一定では気体の体積は粒子数(物質量)に比例する
この3つの法則を組み合わせると、
「気体の体積は圧力に反比例し、絶対温度に比例し、物質量に比例する」
といえます。
これを式として表したものを気体の状態方程式といい、以下のように表します。
PV=nRT
ここで、Rは気体定数と呼ばれる定数で、その値は
8.31×103Pa・L/(mol・K)です。
このことからわかるのは、気体については温度・圧力・体積のうち2つを決めればもう一つは自動的に決定するということです。
例題
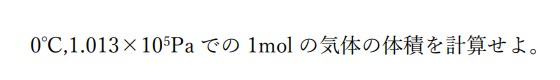
例題の解答

このように気体の状態方程式を利用することで化学基礎で学んだ標準状態での気体の体積が22.4Lであるという事実が計算で導き出せます。
気体の分子量の計算
気体の状態方程式を変形することでその気体の分子量、あるいは平均分子量を求めることができます。
気体分子の物質量は質量÷分子量で表すことができるので、mを気体の質量、Mを分子量として、
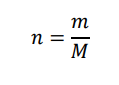
これを気体の状態方程式に代入すると
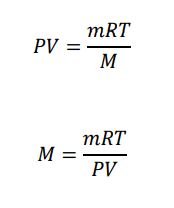
と変形できます。つまり気体の温度、質量、圧力、体積がわかれば分子量を測定することができます。
さらに気体の密度をω[g/L]とすれば、
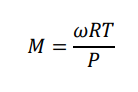
となり(平均)分子量・密度・温度・圧力の関係式が導かれます。
例題
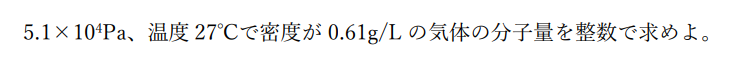
例題の解答
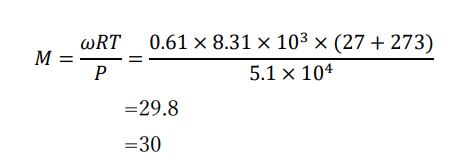
練習問題

練習問題の略解
(1) 8.7L
(2)3.3×106Pa
(3) 1.1g/L


コメント