【物理の基本】ベクトル量・スカラー量とベクトルの計算 | 大学受験模試プロジェクト【模試プロ】

高校物理を学ぶ上で基本となるベクトル量・スカラー量とベクトルの計算について解説します。

特にベクトル量・スカラー量については授業では曖昧に扱うことがおおいようですが、ベクトル量とスカラー量の違いを理解しておくと難問への対応力がかなりつきます。

物理量

科学の世界で扱うときに登場する「量」を物理量といいます。

物理量は扱う現象について様々存在しそれぞれに意味を与える単位があります。

例：速度・質量・力・電流etc

物理量には大きさだけをもつスカラー量と、大きさだけでなく方向ももつベクトル量の2種類があります。

　面積、温度ect

　速度

　速度は「時間当たりにどれだけの距離移動するか」という大きさだけでなく、「北方向」「y軸方向」など方向ももちます。

　変位

　変位は「基準点からどれだけ離れたか」という大きさだけでなく、「基準点からどの方向か」という方向ももちます。

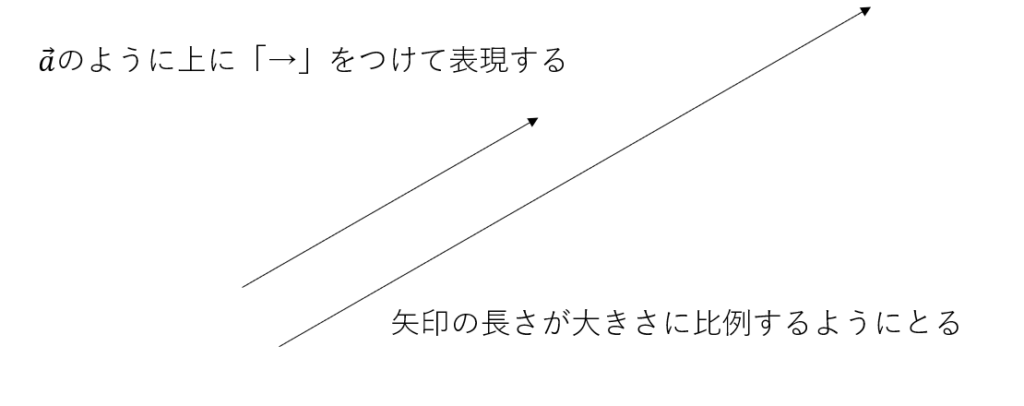
　ベクトル量は大きさだけでなく方向ももつので、単に数字だけではうまく表すことができません。そこで矢印を使い方向と大きさを表します。

　矢印の向きが方向を表し、矢印の長さを大きさに比例するようにとることによって大きさと量を表します。

　数式上で表すときは文字の上に→を書いてベクトルであることを表現します。

スカラー量を計算するときは単に数値を計算すればいいですが、ベクトル量は計算するのに方向を考慮しないといけません。

そのためベクトル量の計算は少々特別な計算になります。

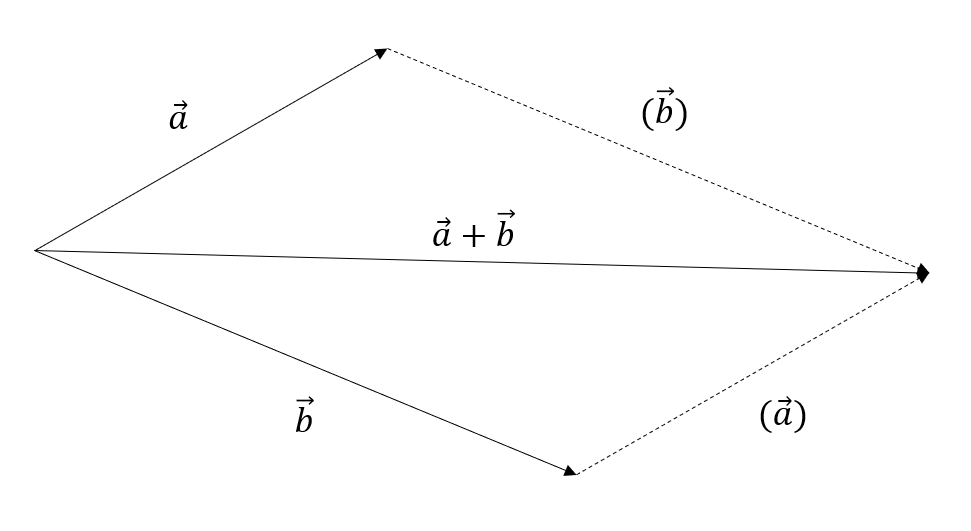
ベクトルの足し算をするときは、平行四辺形の法則を利用します。

足し算したい2つのベクトルを辺とする平行四辺形をつくり、その対角線となる矢印が足し算した結果のベクトルになります。

あるベクトルに対して大きさが等しく、方向が逆方向のベクトルを逆ベクトルといいいます。

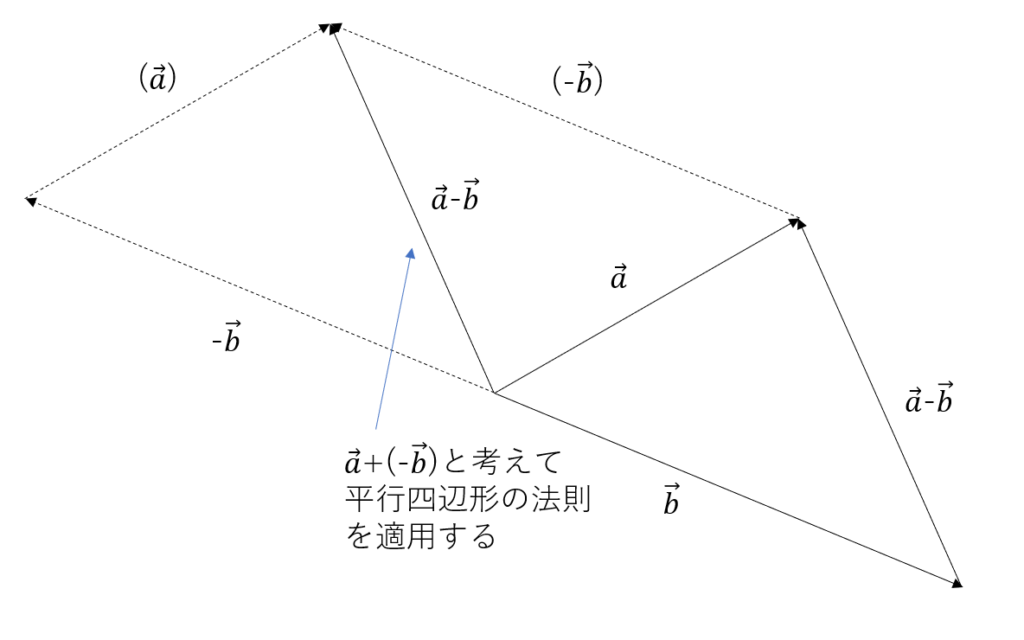
ベクトルの引き算は、

ベクトルを引くことを「逆ベクトルを足すこと」と考えて平行四辺形の法則を適用することで計算できます。

これは「引かれるベクトルの矢印の先端から引くベクトルの矢印の先端まで引いたベクトル」

と同じ意味になります。

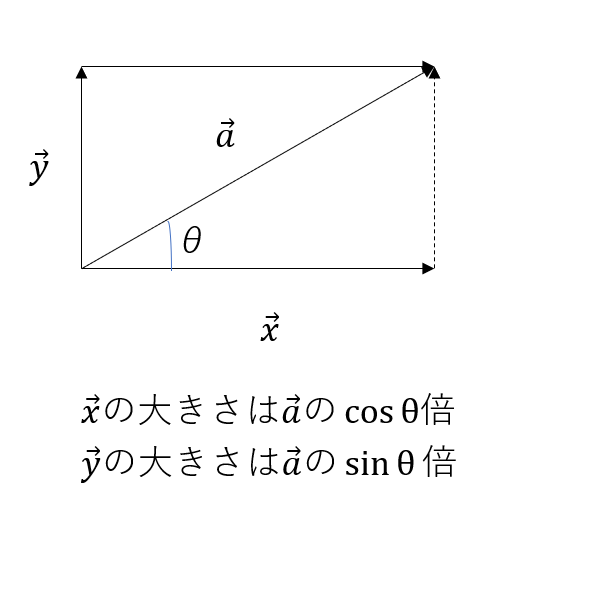
平行四辺形の法則の逆を考えることによって、あるベクトルを2つのベクトルに分解することができます。

物理的には2つの垂直なベクトルに分解することによって考察がうまくいくことが多いです。

図のようにx軸方向のベクトルとy軸方向のベクトルに分解した場合、それぞれのベクトルの大きさは三角比を使って表すことができます。